量子テレポーテーションを回路図と計算式で確認してみよう

今回は量子テレポーテーションについて解説します。問題設定を定義して、量子回路を作成し実際に量子テレポーテーションしているか、計算で確認する方法についての内容です。なお、この記事の読者は、実際に量子コンピューターについて研究しているか、計画中の方を対象としています。

量子テレポーテーションとは

「量子テレポーテーション」とは、量子もつれの効果を使って、一つの量子ビットの状態を別の量子ビットに転送する「情報転送操作」 のことを指します。

「テレポーテーション」と聞いて、瞬間移動が思い浮かぶかと思います。例えば、『ドラゴンボール』で出てくるような瞬間移動です。または、『シン・エヴァンゲリオン劇場版』で、主人公シンジの父ゲンドウが乗るエヴァンゲリオンが裏宇宙で瞬間移動した「量子テレポート」を連想する人もいるかもしれません。しかし、量子テレポーテーションはあくまで情報転送操作であって、瞬間移動ではありません。

また、情報の転送と聞いて「量子ビットをコピーして送りたい別の量子ビットに送ればいいじゃないか」と想像する方もいるかもしれません。しかし量子の世界では、「量子複製不可能（No-Cloning）定理」という量子力学のルールに従って、情報のコピーが原理的に禁止されています。次節では、量子テレポーテーションの「問題設定」について、アリス（Alice）とボブ（Bob）という登場人物を使って定義します。ちなみに、アリスとボブは量子コンピュータの説明でよく出てくる人物名です。

問題設定

量子テレポーテーションの目的はアリスの持つ「量子ビットの情報＝量子状態」をボブの量子ビットにそっくりそのまま転送することです。

「量子ビットの情報＝量子状態」とは
「量子ビットを測定したとき、「0」と「1」それぞれがどのくらいの確率で観測されるか」という測定値の確率分布のことを指します。

アリスからボブに量子状態が転送されればゴール、目的達成です。具体的には、アリスが所有している量子状態$|ψ⟩=α|0⟩+β|1⟩$を、遠く離れた場所にいるボブにそっくりそのまま転送したいわけです。

人によっては、『アリスが途中で$\alpha$と$\beta$の値を盗み見てこっそりボブに電話で
教えればいいのでは？』と思う方もいるかもしれません。しかし、それは不可能です。量子ビットは測定によって量子状態を破壊してしまうからです。

量子テレポーテーションを理解するために必要な知識

量子テレポーテーションを読み解く上で必要な知識は実は多くありません。文中でもその都度確認しますが、以下にあげる4つの知識を頭の片隅にいれておけば十分です。順番に見ていきましょう。
・ 量子状態
・ アダマールゲート（H）
・ CNOT（シーノット）ゲート
・ 測定

量子状態

量子状態＝「量子ビットの0と1それぞれがどのくらいの確率で測定されるか」という確率分布情報のことです。

先ほど1量子ビットの場合の「量子状態」の記法として具体的に
$\Ket{\psi}=\alpha\Ket{0}+\beta\Ket{1}$を使うことを説明しました。

ここではその中身である$\Ket{0}$, $\Ket{1}$が何かを確認しておきます。
$\Ket{0}$：測定により100%「0」を返す量子状態
$\Ket{1}$：測定により100%「1」を返す量子状態

また$\alpha$, $\beta$という係数は$\Ket{\psi}$の中に$\Ket{0}$と$\Ket{1}$がどれぐらいのバランスで入っているかを示す、重みづけ係数のことで、専門的には「確率振幅」と呼ばれます。

アダマールゲート

量子ビットを「重ね合わせ状態＝0と1がランダムで測定される状態」にするのに使う、最重要ゲートです。

具体的には
$\Ket{0}\rightarrow\frac{1}{\sqrt{2}}(\Ket{0}+\Ket{1})$
$\Ket{1}\rightarrow\frac{1}{\sqrt{2}}(\Ket{0}-\Ket{1})$
のような変換を施すゲートです。

CNOTゲート

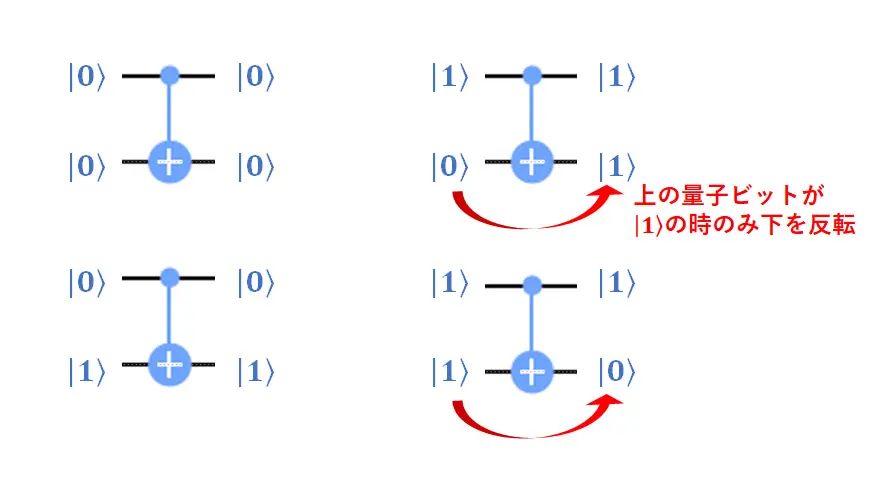
2つの量子ビットに作用する「2量子ビット」の代表例です。以下の図のように、上側の量子ビットが|1⟩のときのみ、下の量子ビットを反転させる効果があります。

便宜的に、上側の量子ビットを「コントロール（制御）」、下側の量子ビットを「ターゲット（標的）」と呼んだりします。

測定

この記号が出てきたら、量子ビットの値を「測定」するものと思ってください。一般に、量子ビットの測定値は、測定するたびに0と1でランダムにばらつきます。「測定」により、0と1どちらが出たかを記録します。

では、準備は最小限にして、実際に問題を解いていきましょう！

量子テレポーテーションを解く

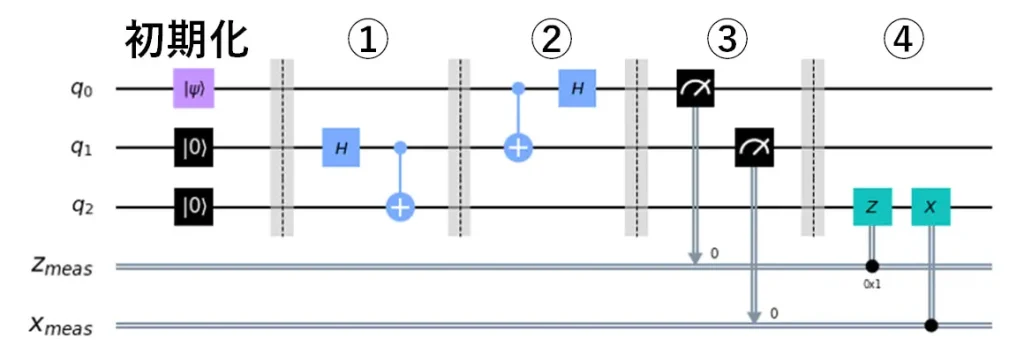
量子テレポーテーションの量子回路は、下図のように書けます。全部で3つある量子ビットについて、各量子ビットの対応（役割）は以下のとおりです。

$q_0$：ボブに転送したい量子状態$\Ket{\psi}=\alpha\Ket{0}+\beta\Ket{1}$を有する量子ビット、アリスが所有
（$q_0$をメッセージ量子ビットと呼ぶことにします）
$q_1$：アリスが所有するもう一つの量子ビット
$q_2$：ボブが所有する量子ビット

この量子回路が操作している概要は以下の通りです。

０.量子ビットを初期化（メッセージ量子ビット$q_0$のみ状態を$\Ket{\psi}$に設定、残りは$\Ket{0}$）
1.アリスとボブの持つ量子ビット対（$q_1$と$q_2$）をもつれさせる
2.アリスは、メッセージ量子ビット$q_0$と自分のもつれ量子ビット$q_1$を相互作用させる
3.アリスは$q_0$と$q_1$を測定し、測定結果をボブに古典通信路で送信
4.ボブはアリスから伝えられた測定結果に応じてX・Zゲートを自分のもつれ量子ビット$q_2$に作用させる

以降本記事では1~4を順番ごとに、計算で丁寧に確認していきます。

１．アリスとボブの持つ量子ビット対（$q_1$と$q_2$）をもつれさせる

まず量子ビット$q_1$と$q_2$の量子もつれ状態を作ります。
（量子もつれについては以下の記事を参照）

図のようにアダマールゲートとCNOTゲートを通すと$q_1$と$q_2$の状態は
$\Ket{B}=\frac{1}{\sqrt{2}}(\Ket{00}+\Ket{11})$になり$\Ket{B}$を「ベル状態（もつれ状態の呼称）」と呼びます。
これにメッセージ量子ビット$\Ket{q_0}$の量子状態$\Ket{\psi}$を掛けた3量子ビットの積は、以下となります。

\begin{eqnarray}
\Ket{\psi} \otimes \Ket{B}
&=&
(\alpha\Ket{0}+\beta\Ket{1}) \otimes \frac{1}{\sqrt{2}}(\Ket{00}+\Ket{11}) \\
&=&
\frac{1}{\sqrt{2}}(\alpha\Ket{000}+\alpha\Ket{011}+\beta\Ket{100}+\beta\Ket{111}) \\
&=&
\frac{1}{\sqrt{2}}(\alpha\Ket{00} \otimes\Ket{0}+\alpha \Ket{01}\otimes\Ket{1}+\beta \Ket{10}\otimes\Ket{0}+\beta \Ket{11}\otimes\Ket{1}) \tag{1}
\end{eqnarray}

２．アリスは、ボブに転送したい量子ビット$q_0$と自分のもつれ量子ビット$q_1$を相互作用させる

その次にまずメッセージ量子ビット$q_0$（状態$\Ket{\psi}$）をコントロール側、
量子ビット$q_1$をターゲット側とする、CNOTゲートを作用させます。

CNOTゲートは、コントロール側が$\Ket{1}$のときのみ、ターゲット側の
$\Ket{0}$と$\Ket{1}$を反転して出力することを思い出しましょう。

前述の式（1）の一番下の右辺は、分かりやすさを重視して$\Ket{q_0q_1}\otimes\Ket{q_2}$の形式で書きましたが、
このうち$\Ket{q_0q_1}$の部分だけを参照すればいいことになります。

CNOTゲートを作用させて変化する3量子ビットの状態は、以下となります。

\begin{eqnarray}
CNOT_{q_{0}, q_{1}}\Ket{\psi} \otimes \Ket{B}
&=&
\frac{1}{\sqrt{2}}
(\alpha\Ket{00} \otimes\Ket{0}+\alpha \Ket{01}\otimes\Ket{1}+\beta \Ket{11}\otimes\Ket{0}+\beta \Ket{10}\otimes\Ket{1}) \\
&=&
\frac{1}{\sqrt{2}}
(\alpha\Ket{0} \otimes\Ket{00}+\alpha \Ket{0}\otimes\Ket{11}+\beta \Ket{1}\otimes\Ket{10}+\beta \Ket{1}\otimes\Ket{01}) \\
&=&
\frac{\alpha}{\sqrt{2}}\Ket{0} \otimes(\Ket{00}+\Ket{11})+\frac{\beta}{\sqrt{2}}\Ket{1} \otimes(\Ket{10}+\Ket{01}) \tag{2}
\end{eqnarray}

次にメッセージ量子ビット$q_0$にアダマールゲートを作用させます。
アダマールゲートは

\begin{equation}
\Ket{0}\rightarrow\frac{1}{\sqrt{2}}(\Ket{0}+\Ket{1})
\end{equation}

\begin{equation}
\Ket{1}\rightarrow\frac{1}{\sqrt{2}}(\Ket{0}-\Ket{1})
\end{equation}

のような変換を施すゲート操作でした。
これを式（2）の$\Ket{q_0}$の量子ビットだけに施せばよいので、計算は以下となります。

\begin{eqnarray}
\cr H_{q_{0}} CNOT_{q_{0}, q_{1}} \Ket{\psi} \otimes \Ket{B}
&=&
\frac{\alpha}{\sqrt{2}}\frac{1}{\sqrt{2}}(\Ket{0}+\Ket{1}) \otimes(\Ket{00}+\Ket{11})+\frac{\beta}{\sqrt{2}}
\frac{1}{\sqrt{2}}(\Ket{0}-\Ket{1}) \otimes(\Ket{10}+\Ket{01}) \\
&=&
\frac{\alpha}{2}(\Ket{000}+\Ket{011}+\Ket{100}+\Ket{111})
+\frac{\beta}{2}(\Ket{010}+\Ket{001}-\Ket{110}-\Ket{101}) \\
&=&
\frac{\Ket{00}(\alpha\Ket{0}+\beta\Ket{1})}{2}+\frac{\Ket{01}(\alpha\Ket{1}+\beta\Ket{0})}{2}+\frac{\Ket{10}(\alpha\Ket{0}-\beta\Ket{1})}{2}+\frac{\Ket{11}(\alpha\Ket{1}-\beta\Ket{0})}{2} \tag{3}
\end{eqnarray}

上右記の式（3）の一番下の右辺が、量子テレポーテーションを理解する上で
最も重要な意味を持ちます。そのため、ここまでの式変形はすべて実際に手を動かして確認してください。

さてここで、量子ビット$q_1$と$q_2$は冒頭のCNOTとアダマールゲートに通すことで、もつれ状態（エンタングルメント）にあったことを思い出してください。その影響を受けて、式（3）も量子ビット同士のテンソル積で記述できない、もつれ状態になっていることが読み取れると思います。

もつれ状態にある量子ビット同士は、片方の測定結果がもう片方の測定結果を確定的に決定する性質を持っていました。そのため、例えばメッセージ量子ビット$q_0$と$q_1$の測定結果が$\Ket{00}$の時、3量子ビットの重ね合わせ状態は壊れて，$q_2$の状態は$\alpha\Ket{0}+\beta\Ket{1}$にジャンプします。これは式（3）の最右辺から読み取れます。

量子もつれ効果による$q_0$と$q_1$の測定結果と、
それにより確定する$q_2$の対応をまとめると以下のようになります。

\begin{eqnarray}
\Ket{q_2}
=
\begin{cases}
\alpha\Ket{0}+\beta\Ket{1} & (\Ket{q_0q_1}=\Ket{00}) \\
\alpha\Ket{1}+\beta\Ket{0} & (\Ket{q_0q_1}=\Ket{01}) \\
\alpha\Ket{0}-\beta\Ket{1} & (\Ket{q_0q_1}=\Ket{10}) \\
\alpha\Ket{1}-\beta\Ket{0} & (\Ket{q_0q_1}=\Ket{11})
\end{cases} \tag{4}
\end{eqnarray}

３．アリスは$q_0$と$q_1$を測定し、測定結果を古典通信路でボブに送信

アリスは自分の手元にある$q_0$と$q_1$を測定します。さらにこの測定結果（つまり$q_0$と$q_1$が0と1のどちらだったか）を古典通信路で送信します。古典通信路とは、要は一般的な連絡ツールのことで、電話やメールなど何でも構いません。例えば測定結果が出たらアリスは電話でボブに結果を教えてあげましょう！

この流れで特筆すべきは、メッセージ量子ビット$q_0$は、測定により量子状態が壊れてしまうということです。

量子テレポーテーションは、量子状態をアリスからボブに転送するものだと説明しましたが、出元のアリス側の量子状態は破壊されていることに注意してください。アリスの持つメッセージ量子ビットの状態を破壊する代わりに、式（4）の量子もつれの威力を利用して、ボブ側の量子ビット$q_2$に量子状態を浮かび上がらせることができるのです！

とてもエレガントです。量子もつれが威力を発揮するとは、こういうことです。

４．ボブはアリスから伝えられた測定結果に応じてX・Zゲートを自身のもつれ量子ビット$q_2$に作用させる

いよいよ仕上げです。

アリスから測定結果を聞いたボブですが、彼は『自分は今どの量子状態の$q_2$を持っているか』を手に取るように把握しています。式（4）のもつれ効果が保証されているからです。

例えばアリスから『測定結果は$\Ket{q_0q_1}=\Ket{10}$だった』と知らされたとします。するとボブは、式（4）に基づいて、自身が持っている$q_2$の量子状態が$\alpha\Ket{0}-\beta\Ket{1}$であると分かります。量子もつれという自然の摂理がボブに教えてくれるのです。

量子テレポーテーションの本来の目的は、量子状態$\Ket{\psi}=\alpha\Ket{0}+\beta\Ket{1}$を
ボブ側の量子ビット$q_2$に転送（再現）することだったので，ボブは最後に$\Ket{1}$の符号をマイナスに反転できれば、目的を達成できます。

つまり量子ビットにZゲートを作用させればよいわけです。Zゲートの役割は$Z\Ket{0}=\Ket{0}$, $Z\Ket{1}=-\Ket{1}$の変換を施すので

\begin{equation}
Z(\alpha\Ket{0}-\beta\Ket{1})=\alpha\Ket{0}+\beta\Ket{1}
\end{equation}

となり、無事量子状態$\Ket{\psi}=\alpha\Ket{0}+\beta\Ket{1}$をボブの持つ$q_2$に再現できました！目的達成です。

式（4）のその他の場合についても同様に$\Ket{\psi}=\alpha\Ket{0}+\beta\Ket{1}$に
変換するための、適切なゲート変換をボブ側で施します。

\begin{eqnarray}
\Ket{q_2}
=
\begin{cases}
\alpha\Ket{0}+\beta\Ket{1}\xrightarrow{何もしない}\alpha\Ket{0}+\beta\Ket{1} & (\Ket{q_0q_1}=\Ket{00})\\
\alpha\Ket{1}+\beta\Ket{0}\xrightarrow{X}\alpha\Ket{0}+\beta\Ket{1} & (\Ket{q_0q_1}=\Ket{01})\\
\alpha\Ket{0}-\beta\Ket{1}\xrightarrow{Z}\alpha\Ket{0}+\beta\Ket{1} & (\Ket{q_0q_1}=\Ket{10})\\
\alpha\Ket{1}-\beta\Ket{0}\xrightarrow{X, Z}\alpha\Ket{0}+\beta\Ket{1} & (\Ket{q_0q_1}=\Ket{11})
\end{cases}
\end{eqnarray}

このようにして、アリスはどれほどボブから離れていたとしても、量子状態を伝えることができます。ちなみに一連の理論は、実験においても実現されています。

量子テレポーテーションの活用の可能性

量子テレポーテーションによって、通信手段が便利になる可能性が示唆されています。

通信のメリットは2つあるとされていて、まず一つ目は、量子状態は超高速で伝えることができるため高速通信が可能になるというメリットです。ただし、目的地に届くまで量子状態を保つ必要があります。現在の研究では、量子状態を長く保つことができ（コヒーレンス時間が長い）遠隔地まで運びやすい光子が用いられています。

もう一つのメリットは、量子複製不可能定理という性質を利用して、原理的に盗聴できないセキュリティーを実現できるというメリットです。量子テレポーテーションによる通信が実現すれば、暗号化しなくてもセキュリティーが保てる未来が来るかもしれません。

脅威？安全？量子コンピューターで暗号が一瞬で解けるのか？ 高速計算が可能な量子コンピューターを使えば、現在主流のRSA暗号も一瞬で破られてしまうのでしょうか？画期的な計算方法「ショアのアルゴリズム」の影響や、次世代の量子暗号の可能性は？暗号技術の面から量子コンピューターについて考えてみました。

実際に手を動かしながら確認することの大切さ

量子テレポーテーションとは「情報転送操作」のことでした。今回の記事では、量子テレポーテーションの問題設定の定義とそれに対応する量子回路を設定し、実際に手計算することで「本当にテレポーテーションする」ことを確認しました。実際に手を動かしながら理論展開を追うと、量子コンピューターについてより理解が深まると思います。

参考文献

▼量子コンピューティング: 基本アルゴリズムから量子機械学習まで、オーム社、嶋田 義皓

▼みんなの量子コンピューター～情報・数理・物理で拓く新しい量子アプリ～
https://www.jst.go.jp/crds/pdf/2018/WR/CRDS-FY2018-WR-09.pdf

▼量子コンピュータが本当にわかる! ― 第一線開発者がやさしく明かすしくみと可能性、技術評論社、武田 俊太郎

▼入門 現代の量子力学 量子情報・量子測定を中心として、講談社、堀田 昌寛

▼Furusawa, Akira, et al. “Unconditional quantum teleportation.” science 282.5389 (1998): 706-709.
https://www.science.org/doi/abs/10.1126/science.282.5389.706

松原 太一

研究員（専門分野：バイオインフォマティクス・深層学習・量子コンピューティング）

2021年から株式会社BlueMemeで量子コンピューティングやゲノム情報解析の研究開発を担当。専門分野は、量子AIの生命医科学への応用。BlueMemeに在籍する傍ら、2023年度より社会人学生として、九州大学大学院システム生命科学府へ進学し博士号取得を目指す。
松原 太一の記事一覧